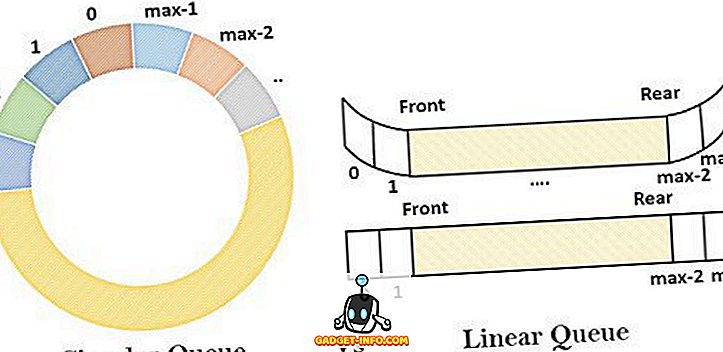
Coada de așteptare poate fi descrisă ca o structură de date liniară non-primitivă, urmând ordinul FIFO în care elementele de date sunt introduse de la un capăt (capătul din spate) și sunt șterse din celălalt capăt (capătul din față). Celelalte variante ale coadă sunt coada circulară, coada de așteptare dublă și coada de priorități.
Diagramă de comparație
| Bazele de comparație | Linear Queue | Coperta circulară |
|---|---|---|
| De bază | Organizează elementele și instrucțiunile de date într-o ordine succesivă una după alta. | Aranjează datele în modelul circular, unde ultimul element este conectat la primul element. |
| Ordine de executare a sarcinii | Sarcinile sunt executate pentru a fi plasate înainte (FIFO). | Ordinul de executare a unei sarcini se poate schimba. |
| Inserare și ștergere | Noul element este adăugat de la capătul din spate și scos din față. | Inserția și ștergerea pot fi efectuate în orice poziție. |
| Performanţă | Ineficace | Funcționează mai bine decât coada liniară. |
Definiția Linear Queue
O coadă liniară este rațional o primă listă în prima ordine. Este așa numită liniară deoarece seamănă cu o linie dreaptă în care elementele sunt poziționate una după alta. Acesta conține o colecție omogenă a elementelor în care se adaugă elemente noi la un capăt și se elimină dintr-un alt capăt. Conceptul de coadă poate fi înțeles prin exemplul unei coadă de audiență care așteaptă în afara tejghelei pentru a obține biletul de teatru. În această coadă, persoana se alătură capătului din spate al coadă pentru a prelua biletul, iar biletul este emis la capătul frontal al coadă.
Există mai multe operații efectuate în coada de așteptare
- În primul rând, coada este inițializată la zero (adică goală).
- Determinați dacă coada este goală sau nu.
- Determinați dacă coada este plină sau nu.
- Introducerea noului element din capătul din spate (Enqueue).
- Ștergerea elementului de la capătul frontal (Dequeue).
Coada de așteptare poate fi implementată în două moduri
- În mod static (utilizând tablouri)
- Dinamic (folosind indicii)
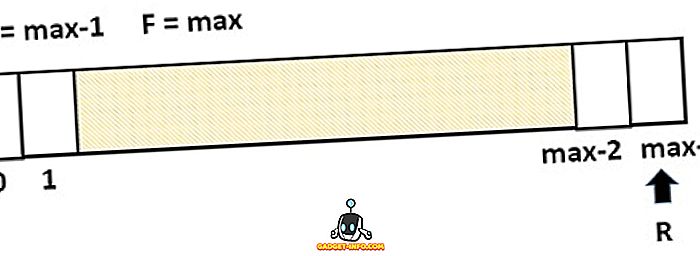
Limitarea coadajului liniar este aceea că creează un scenariu în care nu poate fi adăugat niciun element nou în coadă, chiar dacă coada conține spațiile goale. Această situație de mai sus este ilustrată în figura de mai jos. În acest caz, partea din spate indică ultimul index, în timp ce toate casetele sunt încă goale, nu poate fi adăugat niciun element nou.
Definiția Circular Queue
O coadă circulară este o variantă a coadajului liniar care depășește în mod eficient limitarea coadajului liniar. În coada circulară, elementul nou este adăugat la prima poziție a coadajului dacă ultimul este ocupat și spațiul este disponibil. Când vine vorba de coada liniară, inserarea poate fi efectuată numai de la capătul din spate și ștergerea de la capătul din față. Într-o coadă completă după efectuarea șirului de ștergeri succesive în coadă apare o anumită situație în care niciun element nou nu poate fi adăugat mai departe, chiar dacă spațiul disponibil pentru că există încă condiția de scurgere (Rear = max - 1).
Circulară coadă conectează cele două capete printr-un pointer în care primul element vine după ultimul element. De asemenea, ține evidența frontului și a spatelui prin implementarea unor logici suplimentare pentru a putea urmări elementele care urmează să fie inserate și șterse. Cu aceasta, coada circulară nu generează condiția de depășire până când coada nu este plină în realitate.
Unele condiții urmate de coada circulară:
- Fața trebuie să indice primul element.
- Coada de așteptare va fi goală dacă Front = Spate.
- Atunci când se adaugă un element nou, coada este incrementată cu valoarea unu (Rear = Spate + 1).
- Când un element este șters din coadă, frontul este incrementat de unul (Front = Front + 1).
Diferențele cheie între coada liniară și coada circulară
- Coada liniară este o listă ordonată în care elementele de date sunt organizate în ordinea secvențială. În schimb, coada circulară stochează datele în mod circular.
- Coada liniară urmează ordinului FIFO pentru executarea sarcinii (elementul adăugat în prima poziție va fi șters în prima poziție). În schimb, în coada circulară, ordinea operațiilor efectuate asupra unui element se poate schimba.
- Inserția și ștergerea elementelor este fixată în coada liniară, adică adăugarea de la capătul din spate și ștergerea de la capătul din față. Pe de altă parte, coada circulară este capabilă să introducă și să șteargă elementul din orice punct până când acesta este neocupat.
- Liniile colaterale epuizează spațiul de memorie, în timp ce coada circulară permite utilizarea eficientă a spațiului.
Implementarea coadajului liniar
Algoritmul prezentat mai jos ilustrează adăugarea de elemente într-o coadă:
Coada de așteptare are nevoie de trei variabile de date, inclusiv un singur matrice pentru a stoca coada și altele pentru a stoca poziția inițială față și spate care este -1.
inserați (element, coadă, n, spate) {if (spate == n) apoi imprimați "overflow queue"; altfel {spate = spate + 1; coadă [spate] = element; }} Algoritmul prezentat mai jos ilustrează ștergerea elementelor dintr-o coadă:
delete_circular (element, coadă, spate, față) {if (spate == front), apoi imprimați "underflow queue"; altfel {front = front + 1; element = coadă [față]; }} Implementarea coadajului circular
Un algoritm de interpretare a adăugării elementului în coada circulară:
insert_circular (element, coadă, spate, față) {spate = (spate + 1) mod n; dacă (față == din spate) apoi imprimați "coada este plină"; altceva {coadă [spate] = element; }} Algoritmul explică ștergerea elementului din coada circulară:
delete_circular (element, coadă, spate, față) {if (față == spate) apoi tipăriți ("coada este goală"); altfel {front = front + 1; element = coadă [față]; }} Concluzie
Coada liniară este ineficientă în anumite cazuri în care elementele trebuie să se deplaseze în spațiile libere pentru a efectua operațiunea de introducere. Acesta este motivul pentru care tinde să piardă spațiul de stocare, în timp ce coada circulară folosește în mod corespunzător spațiul de stocare, deoarece elementele sunt adăugate în orice poziție dacă există un spațiu gol.







![social media - Schimbarea tendințelor pe Internet în 2011 [Infographic]](https://gadget-info.com/img/social-media/810/sharing-trends-internet-2011-2.jpg)