Deci, haideți să începem cu diferențele dintre matricea One-dimension și Two-Dimension împreună cu o diagramă de comparație.
Diagramă de comparație:
| Bazele comparației | Unidimensională | Două-dimensional |
|---|---|---|
| De bază | Depozitați o listă unică de elemente de tip de date similare. | Stocați "lista de liste" sau "matrice de matrice" sau "matrice de tablouri dintr-o singură dimensiune". |
| Declaraţie | / * declarație în C ++ tip variabilă nume [dimensiune]; * / / * declarație în Java tip variabilă nume []; variable_name = tip nou [dimensiune]; * / | / * declarație în C ++ tip variabilă [size1] [size2]; * / / * declarație în Java tip variable_name = int int [size1] [size2]; * / |
| Declarație alternativă | / * În Java int [] a = int nou [10]; * / | / * În Java int [] [] a = int nou [10] [20]; * / |
| Dimensiunea totală în octeți | Total Bytes = sizeof (tipul de date al variabilei array) * dimensiunea matricei. | Total Bytes = sizeof (tipul de date al variabilei array) * dimensiunea primului index * dimensiunea celui de-al doilea index. |
| Parametrul de primire | Poate fi recepționat într-un pointer, într-o matrice dimensionată sau într-o matrice neimpozată. | Primirea parametrului trebuie să definească dimensiunea cea mai dreaptă a unui tablou. |
| Dimensiuni | Un dimensional. | Două dimensiuni. |
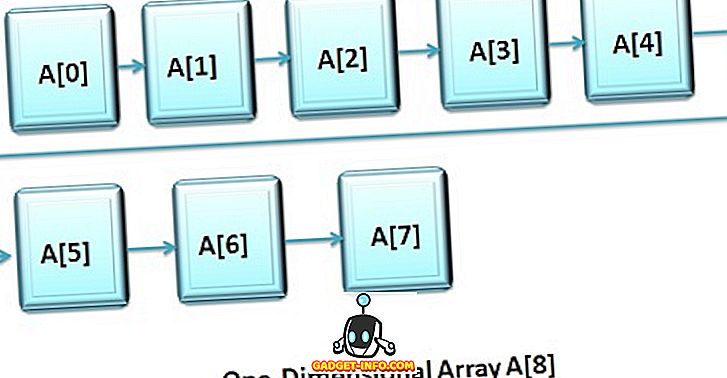
Definiția unidimensional array (1-D array)
Schema unidimensională sau unidimensională este considerată "lista variabilelor de tipuri similare de date" și fiecare variabilă poate fi accesată distinct prin specificarea indexului său în paranteze pătrate precedate de numele acelei matrice.
Să discutăm în contextul C ++
// declarație în tip C ++ variabilă nume [dimensiune];
Aici tip declară tipul de date al variabilei matrice, iar mărimea definește numărul elementului care va păstra matricea.
De exemplu, dacă vrem să declarăm o matrice care va conține soldul fiecărei luni a anului.
// exemplu int month_balance [12];
Balanța pentru o lună este variabila matrice care va conține cele 12 numere întregi, care vor reprezenta soldul fiecărei luni. Acum, dacă vrem să accesăm bilanțul lunii aprilie, trebuie doar să menționăm numele variabilei, urmat de brațul pătrat care conține valoarea indicelui pentru luna aprilie, adică 'month_balance [3]'. Dar, deoarece "aprilie" este a patra lună a anului, dar am menționat "[3]" deoarece toate matricile au 0 ca indicele primului lor element.
În Java, acest lucru se poate face ca
// declarație în Java tip variable_name []; variable_name = tip nou [dimensiune];
Aici, inițial am declarat o variabilă matrice cu tipul ei și apoi am alocat memorie pentru aceasta folosind "new" și asignați "new" la variabila array declarată. Să luăm exemplul de mai sus dacă vrem să declarăm o matrice care va conține soldul în fiecare lună a anului.
// exemplu int luna_balance []; month_balance = int int [12];
Aici, "nou" alocă memoria pentru variabila array "month_balance", deci acum, mont_balance va menține acum memoria pentru 12 valori întregi.
Arhivele pot fi inițializate atunci când sunt declarate. Un inițializator de tablouri este lista de valori separate prin virgule, înconjurată de acolade.
//exemplu
int month_balance = {100, 500, 200, 750, 850, 250, 630, 248, 790, 360, 450, 180}; Definiția arborelui bidimensional (2-D array)
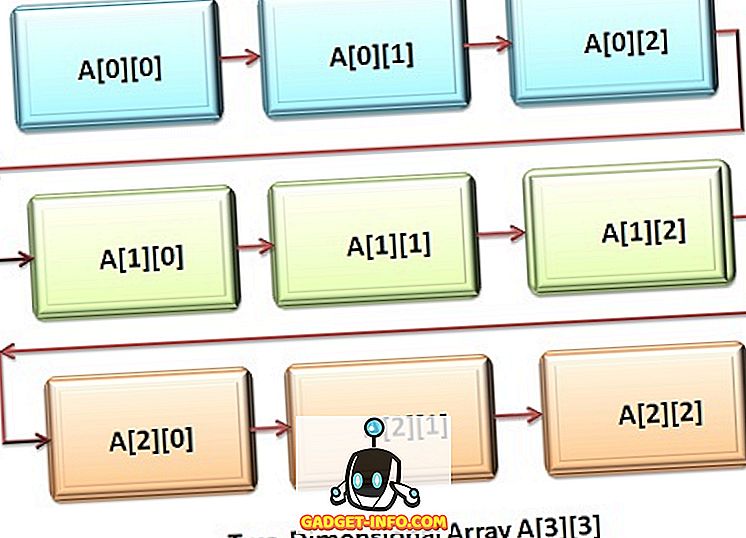
Atât C ++ cât și Java suportă matrice multidimensională. Una dintre formele cele mai simple ale unei matrice multidimensionale este o matrice bidimensională sau o matrice 2-D. O matrice bidimensională poate fi considerată ca "matrice de matrice" sau "matrice de matrice unidimensionale". Pentru a declara variabila matriceală bidimensională, trebuie să specificăm numele matricei, urmat de două paranteze pătrate, unde al doilea indice este al doilea set de paranteze pătrate.
O matrice bidimensională este stocată sub forma matricei rând-coloană, unde primul indice indică rândul, iar al doilea indice indică coloana. Indicele al doilea sau cel din dreapta al unei matrice se modifică foarte rapid în comparație cu primul sau cel mai stâng index în timp ce accesează elementele unei matrice.
// declarație în tip C ++ variable_name [size1] [size2];
De exemplu, vrem să stocăm soldul la fiecare 30 de zile în fiecare lună a anului, într-o matrice 2-D.
// exemplu int month_balance [12] [30];
În Java, matricea bidimensională este obținută prin
// declarație în Java tip variable_name = new int [size1] [size2]; // exemplu int luna_balance = int int [12] [30];
Deoarece nu putem trece întreaga matrice ca parametru pentru o funcție, este trecut un indicator la primul element al matricei. Un argument care primește matricea bidimensională trebuie să definească dimensiunea cea mai potrivită. Dimensiunea cea mai din dreapta este necesară deoarece compilatorul are nevoie de aceasta, pentru a confirma lungimea fiecărui rând dacă dorește să indexeze corect matricea. Dacă nu este menționat cel mai bun indice, compilatorul nu poate determina unde începe rândul următor.
// exemplu în Java void receiveing_funct (int a [] [10]) {. . . } Atunci când memoria este alocată dinamic matricei bidimensionale din Java, se specifică indexul cel mai stâng și dimensiunile rămase pot fi alocate separat, adică toate rândurile matricei pot să nu aibă aceeași dimensiune.
// exemplu în Java int month_balance = new int [12] []; month_balance [0] = int int [31]; month_balance [1] = nou int [28]; month_balance [2] = int int [31]; month_balance [3] = nou int [30]; month_balance [4] = int int [31]; month_balance [5] = int nou [30]; month_balance [6] = nou int [31]; month_balance [7] = nou int [30]; month_balance [8] = int int [31]; month_balance [9] = int int [30]; month_balance [10] = int int [31]; month_balance [11] = nou int [30]; month_balance [12] = int int [31];
Dar nu există niciun avantaj de a face acest lucru.
Diferențe cheie între matricea unidimensională și bidimensională
- Gama unidimensională este o listă a cărei elemente sunt de tip dat de același tip. Pe de altă parte, matricea bidimensională este o listă a cărei elemente sunt matrice de tip de date similar.
- În C ++, atunci când matricea unidimensională este recepționată de parametrul unei funcții de recepție, nu este necesar să se menționeze dimensiunea matricei, deoarece compilatorul înțelege că matricea de tip (tipul de date menționat împreună cu parametrul) cu o anumită lungime urmează să fie primită. Într-o matrice bidimensională, se specifică cel de-al doilea sau cel mai bun indice, deoarece compilatorul trebuie să știe unde începe un rând cu un singur rând și un rând nou.
- În C ++, matricea unidimensională este stocată într-o locație de memorie contiguă în ordinea indexată, în timp ce matricea bidimensională este de asemenea stocată în locația de memorie contiguă, dar deoarece există mai multe rânduri într-o matrice bidimensională, stocarea un prim rând este urmat de un al doilea și al treilea și așa mai departe.
Notă:
Trecerea atât a matricei unidimensionale, cât și a matricei bidimensionale la o funcție este similară, adică ambele sunt transmise numai de numele matricei
// exemplu passing_funt (nume_de_array);
Concluzie:
În ambele matrice unidimensionale și bidimensionale, indexul joacă un rol foarte important, deoarece este singurul lucru care identifică în mod specific un element din matrice. Atât matricea unidimensională, cât și cea bidimensională pot fi inițializate în momentul declarației lor.
